欢迎来客！ 要启用所有功能，请联系我们。
什么是变换矩阵以及如何使用它 - 本文解释什么是变换矩阵以及它为何如此工作。
Paul Rayman
发布于： 四年前
什么是转换矩阵以及如何使用它
矩阵简介
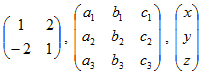
.png)
.png)
减法
.png)
.png)
.png)
.png)
.png)
.png)
.png)
除法
.png)
.png)
.png)
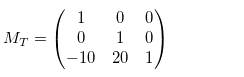
.png)
.png)
比例
.png)
.png)
.png)
翻转/反射
.png)
.png)
旋转
.png)
.png)
.png)
.png)
剪切
.png)
.png)
.png)
.png)
多重转换
.png)
.png)
.png)
总结
当您使用 PDFium 库处理 PDF 文件中的对象时，您可以使用 SetMatrix 函数以多种方式转换对象（通常是图像，但也可以是任何其他嵌入对象）。 使用变换矩阵，您可以旋转、平移（移动）、缩放或剪切图像。 可以在此处找到使用矩阵将图像缩放到 PDF 文档中页面大小的示例。
本文对什么是转换矩阵以及它为何如此工作提供了更深入的解释。
如果您对线性代数很陌生，矩阵只是一组值，它们组合在一起形成一个矩形或正方形形式。 以下是矩阵示例：
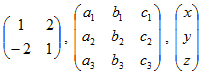
许多物理值可以（并且经常）以矩阵形式表示。 例如，坐标； 它们通常表示为一个向量——一个具有一列的矩阵和每个空间维度的行数（2 行表示 2D，3 行表示 3D，依此类推）。 这种矩阵中的每个元素都是相应轴上的坐标。 向量的示例如上所示。
PDF 文档也使用坐标系。 两个轴是页面的垂直和水平尺寸，每个坐标代表该轴上的 PDF 点数。 因此，如果页面上的给定对象放置在距底部 3500 点和距左侧 100 点的位置，则其坐标向量为：
这基本上是相同的。
矩阵可以像普通数字一样进行求和、减法、乘法和除法（反转）。 加法和减法是最简单的操作，下面是示例：
加法
要将一个矩阵添加到另一个矩阵，您只需将第一个矩阵的每个元素添加到第二个矩阵的相应元素即可。 当然，矩阵必须具有相同的维度。
减法
除了算术符号外，减法也一样：
加法和减法是可交换的。 您可以更改矩阵的顺序并仍然得到相同的结果（减法时的算术符号除外）：
其中 A 和 B 是矩阵。
乘法
矩阵相乘是一个更棘手的过程。 要将矩阵 A 与矩阵 B 相乘，您应该将第一个矩阵的每一行乘以第二个矩阵的每一列。 每个这样的乘积都是结果矩阵在 (i, j) 位置的元素。 其中 i 是 A 中行的索引，j 是 B 中列的索引。
听起来很复杂？ 这是一个例子：
首先，我们将第一个矩阵的第一行乘以第二个矩阵的第一列。 这为我们提供了结果矩阵的 (1,1) 处的元素：
然后，我们将第二行和第一列相乘以计算 (1,2) 处的元素：
然后，我们计算 (2,1) 处的元素：
最后是 (2,2) 处的元素：
矩阵相乘的方式有两个重要影响：
- A 的列数必须与 B 的行数匹配。您可以使用多个 2×2 和 2×2 矩阵，如上所示。 您还可以将 2×6 到 4×2（产生 6×4 矩阵）或 3×3 到 1×3（产生 3×3 矩阵）的倍数 . 但是，例如，您不能将 3×3 乘以 1×2。
- 矩阵的乘法不是可交换的。 那是img10。 如果您采用上面的示例并更改矩阵的顺序，结果会有所不同，即：
除法
如果您认为矩阵的乘法很难理解，那么我们要告诉您一个坏消息：它们的除法更加棘手。 但是，还有一个好消息：您不需要分割矩阵来执行 PDF 对象的转换，所以我们简单地留下这个维基百科链接 JFYI：https://en.wikipedia.org/wiki/Invertible_matrix
什么是变换矩阵
PDF 在二维坐标系中表示其内容。 每个点的坐标都可以表示为一个向量：(x, y)。 转换矩阵允许更改默认坐标系并将原始坐标 (x, y) 映射到这个新坐标系：(x', y')。 根据我们改变坐标系的方式，我们以这种方式有效地旋转、缩放、移动（平移）或剪切对象。
变换矩阵是一个 3×3 矩阵：
矩阵的元素对应于各种变换（见下文）。 要变换坐标系，您应该将原始坐标向量乘以变换矩阵。 由于矩阵是 3×3，向量是 1×2，我们需要向它添加一个元素，以使向量的大小与乘法规则所要求的矩阵相匹配（见上文）。
话虽如此，转换后的向量如下获得：
例如，要在页面的位图上旋转图像，PDF 渲染器应获取图像每个点的坐标，使用上述公式更改它们并在新坐标处渲染该像素。
这就是您调用 SetMatrix 函数时所做的事情：您告诉渲染器它应该如何转换对象的每个渲染像素。
变换操作
平移
平移操作将坐标系移动给定的偏移量。 该操作会产生一个新的坐标系，该坐标系从原始坐标系沿 x 轴移动 e 并沿 y 轴移动 f。
平移操作的变换矩阵为：
例子：
原始坐标系中点的坐标为 (240 651 1)。 我们希望将坐标系向左平移 10 点，向上平移 20 点。 所需的变换矩阵为：
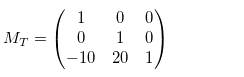
然后得到的坐标是：
如您所见，坐标已按计划更改。 以相同的方式转换图像的所有其他像素。
传递给 SetMatrix 方法的参数是：
代码：
比例
要缩放一个对象，我们需要更改其尺寸之一或两者。
缩放操作的变换矩阵为：
其中 a 和 d 分别是水平和垂直比例因子。 如果它们大于 1，则按比例放大对象。 如果它们小于 1，则对象从其原始大小按比例缩小。
例子：
该矩阵将沿 x 轴将对象放大 40%，沿 y 轴缩小 20%。
代码：
翻转/反射
此操作类似于缩放。 我们只需要反转水平/垂直翻转的坐标之一或两者都反转以反映原点。
水平翻转：
代码：
垂直翻转：
代码：
中央翻转：
代码：
旋转
旋转操作将原始坐标系顺时针或逆时针旋转给定角度。
旋转操作的矩阵是：
其中 img09 是旋转角度。
矩阵的形式来源于简单的三角函数，但形式证明超出了本文的范围。
假设我们要将对象顺时针旋转 30 度。 然后，对象的每个像素被变换如下：
代码：
剪切
x 方向剪切的变换矩阵为：
假设我们要将对象向右剪切 20 个 PDF 点：
代码：
对于 y 方向的剪切：
要将对象向下剪切 45 个 PDF 点：
代码：
多重转换
如果您需要对同一个对象应用多个转换怎么办？ 比如，放大和旋转？ 或者水平翻转镜像图像并将其转换到页面上的所需位置？
在这种情况下，您只需要几个转换矩阵。 为了执行一系列变换，将各个变换的矩阵相乘。 然而，如上所述，乘法运算不是可交换的，因此变换矩阵的顺序有很大的不同。
例如，如果要旋转对象，然后平移它，则生成的变换矩阵为：
对于变换矩阵的倒序，得到的矩阵是不同的：
第一次可能看起来并不明显。 您可以将对象移动 10 个点，然后将其旋转 45 度。 或者您可以将其旋转 45 度，然后将旋转的对象移动 10 个点。 为什么有区别？ 因为变换矩阵不旋转（平移、缩放等）对象，所以它旋转包含对象的坐标系。
这样想吧。 把铅笔放在桌子上。 当您变换对象时，变换顺序将是“将铅笔旋转 45 度，然后将其向左移动 10 厘米”。 但是当你变换坐标系时，你会得到“将桌子旋转 45 度，然后将桌子向左移动 10 厘米”。
总结
现在您知道 Matrix 类中的这些 a、b、c、d、e 和 f 系数是什么意思了。 由这些元素组成的变换矩阵允许几乎任意调整任何 PDF 位图或其他对象。
由用户3 年前编辑 | 原因：未指定
由用户3 年前编辑 | 原因：未指定
COGITO SOFTWARE CO., LIMITED版权所有
